Code 備忘錄►Graph

TIOJ::IOI::1889 . 【IOI2015】Towns 一堆糖

http://tioj.ck.tp.edu.tw/problems/1889
這題是IOI 2015 Day2的題目，還是台灣教授出的題目。
結果反而這題在賽中台灣隊死的很慘QQ。
題目是怪怪圖論互動題。

題目給你一棵樹，但是卻沒告訴你樹長怎樣，取而代之的，他告訴你樹有幾個葉子。
現在他讓你詢問樹上任意兩個葉子的距離，他要你求出兩個東西。
第1個就是，找出樹上一個點，他距離最遠的葉子的距離最近，請找出這個距離，我們稱他為樹半徑。另外，這個點在這題稱為樞紐，我們就先稱他為CBD吧。
第2個要問的是，對於這個CBD，如果以他為根節點，他的每個子樹的葉子數量不超過全部葉子的一半（小於等於n/2），我們就稱他為平衡的，輸出R，否則輸出負R（R就是第1個問題的半徑長度）。

這題一開始我完全沒有想法，沒什麼接觸過這種題目，題目又太跳脫了。
題目會限制我們查詢的次數，正解的次數是7n/2。
分開慢慢想，對於第一個問題，很顯然要先找出樹直徑，找出樹直徑的方法就是先對每一個點都查到點0的距離，選最長的點s，再對s做一次找最遠的點t，s到t就是直徑，這時我們已經可以求出每個點連到0-s這條鍊上的位置了，怎麼做呢？

假設點i在距離點s Si的地方接上了0-s鍊，這個接點到點i的距離是Di，到點0的距離是tmp（後面用不到），我們可以列出三個方程式，設兩點距離是L（i,j）。
$ Si + tmp = L(0,s) $
$ tmp + Di = L(0,i) $
$ Si + Di = L(i,s) $
其中我們發現，這3個方程式的L（）距離我們早就查詢過了，如果我們先開一個二維陣列快取查詢過的答案，那這幾個查詢不會浪費查詢次數。

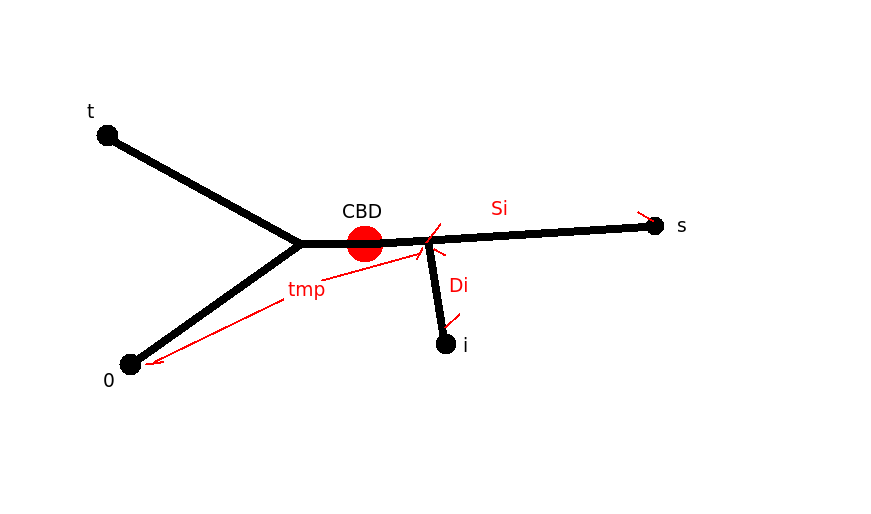
把每個點的這3個方程式算出來，我們可以得到，每個點i到0-s鍊的距離Di，和這個接點到s的距離Si，而我們知道CBD會在s-t鍊上，而且也會在0-s上（因為0接到s-t上的時候，會走向比較遠的那一端，也就是s，所以CBD一定在靠s這邊）。所以每個點的Si就和（直徑s-t鍊長度 - Si）取max就是這個點距離最遠的點的距離，然後這個值最小的點就是CBD。

這樣我們就做完第一個問題了，在做第二個之前，我們要先知道，我們可能會找出兩個CBD，因為只要直徑中間一條邊的兩端出去深度都一樣就會這樣。
所以做第二個問題前，我們要先判段要選哪一個當CBD。我們可以透過Si小於等於比較靠近S的那個CBD的Si，來知道如果不選這個點當CBD，至少我們會得到一個多少點的子樹，如果找到發現大於n/2，那就一定要選這個點當CBD，因為另外一個不可能平衡了，不然就試試看另外那個，因為這個不可能了（有多於n/2的點再他那邊，選自己不可能平衡），或是兩邊都是n/2，那一定平衡，不過這個不判也不會怎樣。

所以我們現在已經選定了，之後我們就可以開始驗證CBD是否平衡。
我們需要轉化一下問題，我們先想想怎麼查詢兩個點在不在以CBD為根的樹的同一個子樹上，首先我們可以確定如果他們的Si和CBD的Si不一樣，那如果都在CBD的同一邊（都小於CBD的Si或是都大於CBD的Si），那就是同一棵，不然就不是同一棵;如果他們的Si都和CBD的Si一樣，那就看看他們之間的距離，和他們到0-s鍊的距離和是否相同，如果相同代表在不同棵子樹，不然他們一定是先會合在一起連到0-s鍊。也就是說如果符合：
$ Di + Dj \neq L(i,j) $
他們就會在不同子樹上。

有了這個判斷的方式後，我們想要透過判斷兩兩是否在同一棵子樹的方式來確定是否有一棵子樹葉子多於n/2。
問題可以變成，讓你查詢一堆數字是否相等，你要告訴我這些數字中是否存在絕對眾數（數量大於n/2的數）。
這個有很多作法，有論文用了兩個Stack法，我完全沒有感覺，只是覺得他很對。
不過我有一個更好玩的作法，打架法。

首先先把數字分成N組，每組都是一個人，然後奇數的組別和偶數的組別對打，如果最後還剩下一組奇數的組別，直接晉級。對打時，一隊派一人，兩人會一起死掉然後去墓地，兩隊不停的打，直到有一隊或是兩隊都沒人了，如果有剩下人就晉級。如果兩隊在查詢後發現是一樣的（用上面說的查詢去查），那就直接合併這兩組，人數相加，然後直接晉級。第二輪再重複上面的過程，直到剩下1組或是0組，如果是0組，代表絕對多數不存在（因為互相對打都死光了），剩下1組的話，絕對多數可能存在，但是不確定，必須拿這個數字去墓地裡驗證，看有哪些屍體和他是同一個數字，可是在遇到之前就被別人殺掉了，這樣其實也就是直接統計這個數字在集合裡的總數，如果大於n/2就是有絕對眾數，也就是原本的題目中的CBD不平衡，要輸出負數。

依照題目規定，因為我們一開始找第一個答案會用掉約2n次，所以我們第二個答案只有3n/2次可以用，打架第一輪如果直接死光了話，我們只會花n/2次，如果都成功合併晉級了，那我們之後墓地裡的屍體數量就會少一半（雖然我剛剛說一個一個打，但是很顯然我們對於已經知道是同組的屍體不需要分開比較，可以一起比），所以基本上次數可以控制在3*n/2裡，很神奇吧！

這樣就做完了，我再重新敘述一次打架的流程好了。

首先，有K組數字，每組有Pi個人，如我人數一樣，直接兩組丟進墓地，如果不一樣，小的那組直接進墓地，大的那組要把跟小的那組一樣的人數送進墓地，然後剩下的晉級，如果兩組人比較後發現是同一組的，那就合併晉級。
最後剩下0組就直接結束，剩下1組就拿這組去跟墓地裡的每組檢查，一樣就計算人數，看看有沒有超過一半，以上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
#include <bits/stdc++.h>
#include "lib1889.h"
#define F(n) Fi(i,n)
#define Fi(i,n) Fl(i,0,n)
#define Fl(i,l,n) for(int i=l;i<n;i++)
using namespace std;
const int N = 111;
map<int,int> H;
int D[N], S[N];
typedef pair<int,int> PII;
int getL(int a,int b){
    static int cache[N][N];
    if(a == b){
        if(a==-1)memset(cache,0,sizeof(cache));
        return 0;
    }
    if(a>b)swap(a,b);
    int &tmp = cache[a][b];
    if(tmp)return tmp;
    return tmp = getDistance(a,b);
}
int getFP(int now, int n){
    int mx = 0, res;
    F(n)if(i!=now){
        if(mx < getL(now,i)){
            mx = getL(now,i);
            res = i;
        }
    }
    return res;
}
void get3ANS(int &x,int &y,int &z,int fi,int se,int th){
    int sum = (fi+se+th)/2;
    x = sum - se;
    y = sum - th;
    z = sum - fi;
}
bool equal(int a,int b,int CBD){
    if(S[a]==CBD&&S[b]==CBD){
        return D[a]+D[b] > getL(a,b);
    }else{
        if(S[a]==CBD||S[b]==CBD)return false;
        return S[a]<CBD!=S[b]>CBD;
    }
}
bool fight(int CBD, int n){
    vector<PII>JIZZ,F1,F2;
    F(n)F1.push_back(PII(i,1));
    while(F1.size()>1){
        F(F1.size()/2){
            PII a = F1[i*2], b = F1[i*2+1];
            if(equal(a.first,b.first,CBD)){
                F2.push_back(PII(a.first,a.second+b.second));
            }else if(a.second == b.second){
                JIZZ.push_back(a);
                JIZZ.push_back(b);
            }else{
                if(a.second>b.second)swap(a,b);
                JIZZ.push_back(a);
                JIZZ.push_back(PII(b.first,a.second));
                F2.push_back(PII(b.first,b.second-a.second));
            }
        }
        if(F1.size()&1)F2.push_back(F1.back());
        F1.swap(F2);
        F2.clear();
    }
    if(F1.empty())return 0;
    int cnt = F1[0].second;
    for(PII p:JIZZ){
        if(equal(F1[0].first,p.first,CBD))cnt += p.second;
    }
    return cnt*2 > n;
}
main(){
    while(1){
        int n = Init(),s,t,L;
        H.clear();
        getL(-1,-1);//init cache[N][N];
        s = getFP(0,n);
        t = getFP(s,n);
        L = getL(s,t);
        F(n){
            int tmp;
            get3ANS(S[i],tmp,D[i],getL(0,s),getL(0,i),getL(i,s));
            H[S[i]] ++;
        }
        auto p = H.upper_bound(L/2);
        int CBD1 = p->first;
        int CBD2 = prev(p)->first;
        int CBD;
        if(max(L-CBD1,CBD1) == max(L-CBD2,CBD2)){
            int cnt = 0;
            for(auto p:H){
                if(p.first <= CBD2)cnt+=p.second;
                else break;
            }
            CBD = cnt*2<n?CBD1:CBD2;
        }else{
            CBD = max(L-CBD1,CBD1) < max(L-CBD2,CBD2)?CBD1:CBD2;
        }
        int R = max(L-CBD,CBD);
        answer(fight(CBD,n)?-R:R);
    }
}